Задание 16. (А. Кабанов, 2024)
Задание 16. (А. Кабанов, 2024)
Умскул: Основы Python для ЕГЭ (конспект)
Решение Заданий 16 с помощью словарей, Л. Шастин
Задание 16. (А. Кабанов, 2024)
Задание 16. (А. Кабанов, 2024)
Решение Заданий 16 с помощью словарей, Л. Шастин
Рекурсивный алгоритм задан следующим образом:
def f(n):
if n < 3: print('*')
else:
f(n - 1)
f(n - 2)
f(n - 2)
Сколько звездочек напечатает эта процедура при вызове F(6)? В ответе запишите только целое число.
21
Вариант 1:
def f(n):
global k
if n < 3: k += 1
else: f(n - 1); f(n - 2); f(n - 2)
k = 0; f(6)
print(k)
Вариант 2:
f = {1:1, 2:1}
for n in range(3, 7): f[n] = f[n - 1] + f[n - 2] + f[n - 2]
print(f[6])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1 F(n) = F(n–1) * n, при n > 1
Чему равно значение функции F(5)? В ответе запишите только целое число.
120
Вариант 1:
def f(n):
if n == 1: return 1
return f(n - 1) * n
print(f(5))
Вариант 2:
f = {1:1}
for n in range(2, 6): f[n] = f[n - 1] * n
print(f[5])
Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1; G(1) = 1; F(n) = F(n – 1) – G(n – 1), G(n) = F(n–1) + G(n – 1), при n >=2
Чему равно значение величины F(5) / G(5)? В ответе запишите только целое число.
1
Вариант 1:
def f(n):
if n == 1: return 1
return f(n - 1) - g(n - 1)
def g(n):
if n == 1: return 1
return f(n - 1) + g(n - 1)
print(f(5) / g(5))
Вариант 2:
f = {1:1}; g = {1:1}
for n in range(2, 6):
f[n] = f[n - 1] - g[n - 1]
g[n] = f[n - 1] + g[n - 1]
print(f[5] / g[5])
Дан рекурсивный алгоритм:
def f(n):
print('*')
if n > 0: f(n - 2); f(n // 2)
Сколько символов "звездочка" будет напечатано на экране при выполнении вызова F(7)?
21
Вариант 1:
def f(n):
global k; k += 1
if n > 0: f(n - 2); f(n // 2)
k = 0; f(7)
print(k)
Вариант 2:
f = {-1:1, 0:1}
for n in range(1, 8): f[n] = 1 + f[n - 2] + f[n // 2]
print(f[7])
Дан рекурсивный алгоритм:
def f(n):
print(n)
if n < 6: f(n + 2); f(n * 3)
Найдите сумму чисел, которые будут выведены при вызове F(1).
79
Вариант 1:
def f(n):
global s; s += n
if n < 6: f(n + 2); f(n * 3)
s = 0; f(1)
print(s)
Вариант 2:
f = {n:n for n in range(6, 50)}
for n in range(5, 0, -1): f[n] = n + f[n + 2] + f[n * 3]
print(f[1])
Дан рекурсивный алгоритм:
def f(n):
print(n)
if n < 5: f(n + 1); f(n + 3)
Найдите сумму чисел, которые будут выведены при вызове F(1)
49
Вариант 1:
def f(n):
global s; s += n
if n < 5: f(n + 1); f(n + 3)
s = 0; f(1); print(s)
Вариант 2:
f = {n:n for n in range(5, 50)}
for n in range(4, 0, -1): f[n] = n + f[n + 1] + f[n + 3]
print(f[1])
Ниже записаны две рекурсивные процедуры: F и G:
def f(n):
if n > 0: g(n - 1)
def g(n):
print('*')
if n > 1: f(n - 2)
Сколько символов «звёздочка» будет напечатано на экране при выполнении вызова F(11)?
4
Вариант 1:
def f(n):
if n > 0: g(n - 1)
def g(n):
global k; k += 1
if n > 1: f(n - 2)
k = 0; f(11); print(k)
Вариант 2:
f = {-1:0, 0:0}; g = {0:1}
for n in range(1, 12):
f[n] = g[n - 1]
g[n] = 1 + f[n - 2]
print(f[11])
Ниже записана рекурсивная процедура:
def f(n):
if n > 1:
f(n - 4)
print(n)
f(n // 2)
Что будет напечатано на экране при выполнении вызова F(11)?
3731152
def f(n):
if n > 1:
f(n - 4)
print(n, end = '')
f(n // 2)
f(11)
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = 1 при n = 1, F(n) = n + 2 + F(n – 1), если n чётно, F(n) = 2 ⋅ F(n – 2), если n нечётно
Чему равно значение функции F(24)?
2074
Вариант 1:
def f(n):
if n == 1: return 1
return n + 2 + f(n - 1) if n % 2 == 0 else 2 * f(n - 2)
print(f(24))
Вариант 2:
f = {1: 1}
for n in range(2, 24 + 1):
f[n] = n + 2 + f[n - 1] if n % 2 == 0 else 2 * f[n - 2]
print(f[24])
Определите, сколько символов * выведет эта процедура при вызове F(22):
def F( n ):
print('*')
if n >= 1:
print('*')
F(n-1)
F(n-2)
F(n-3)
1957585
В данной программе НЕЛЬЗЯ!!! применять декоратор lru_cache, т.к. вместо того, чтобы выполнять пользовательскую функцию и увеличивать значение k, программа будет брать уже вычисленные значения из cache, а значит, значение счетчика увеличиваться не будет (хорошо демонстрирует уменьшение количества необходимых вычислений)
Вариант 1:
def f(n):
global k; k += 1
if n >= 1: k += 1; f(n - 1); f(n - 2); f(n - 3)
k = 0; f(22); print(k)
Вариант 2:
f = {-2:1, -1:1, 0:1}
for n in range(1, 23): f[n] = 1 + 1 + f[n-1] + f[n-2] + f[n-3]
print(f[22])
Определите наименьшее значение n, при котором сумма чисел, которые будут выведены при вызове F(n), будет больше 500000. Запишите в ответе сначала найденное значение n, а затем через пробел – соответствующую сумму выведенных чисел.
def F( n ):
print(2*n)
if n > 1:
print(n-5)
F(n-1)
F(n-2)
24 531864
В данной программе НЕЛЬЗЯ!!! применять декоратор lru_cache, т.к. вместо того, чтобы выполнять пользовательскую функцию и увеличивать значение k, программа будет брать уже вычисленные значения из cache, а значит, значение счетчика увеличиваться не будет (хорошо демонстрирует уменьшение количества необходимых вычислений)
Вариант 1:
def f(n):
global s; s += 2 * n
if n > 1: s += n - 5; f(n - 1); f(n - 2)
for n in range(1, 100):
s = 0; f(n)
if s > 500_000: print(n, s); break
Вариант 2:
f = {0:0, 1:2}
for n in range(2, 10 ** 6):
f[n] = 2 * n + (n - 5) + f[n - 1] + f[n - 2]
if f[n] > 500_000: print(n, f[n]); break
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = 1 при n = 1, F(n) = n + F(n – 1), если n чётно, F(n) = 2 ⋅ F(n – 2), если n > 1 и n нечётно
Чему равно значение функции F(26)?
4122
Вариант 1:
def f(n):
if n == 1: return 1
if n % 2 == 0: return n + f(n - 1)
return 2 * f(n - 2)
print(f(26))
Вариант 2:
f = {1:1}
for n in range(2, 27): f[n] = n + f[n - 1] if n % 2 == 0 else 2 * f[n - 2]
print(f[26])
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = 2 ⋅ n при n ≤ 5 F(n) = F(n – 2) + 3 ⋅ F(n / 2) + n, если n > 5 и чётно, F(n) = F(n – 1) + F(n – 2) + F(n – 3), если n > 5 и нечётно
Чему равно значение функции F(99) + F(100)?
142139494
Вариант 1:
def f(n):
if n <= 5: return 2 * n
if n % 2 == 0: return f(n - 2) + 3 * f(n // 2) + n
return f(n - 1) + f(n - 2) + f(n - 3)
print(f(99) + f (100))
Вариант 2:
f = {}
for n in range(1, 5 + 1): f[n] = 2 * n
for n in range(6, 101):
if n % 2 == 0: f[n] = f[n - 2] + 3 * f[n // 2] + n
else: f[n] = f[n - 1] + f[n - 2] + f[n - 3]
print(f[99] + f[100])
Алгоритм вычисления функций F(n) и G(n) задан следующими соотношениями:
F(1) = G(1) = 1 F(n) = 2 ⋅ F(n – 1) + G(n – 1) – 2, если n > 1 G(n) = F(n – 1) + 2 ⋅ G(n – 1), если n > 1
Чему равно значение F(14) + G(14)?
1594324
Вариант 1:
def f(n):
if n == 1: return 1
return 2 * f(n - 1) + g(n - 1) - 2
def g(n):
if n == 1: return 1
return f(n - 1) + 2 * g(n - 1)
print(f(14) + g(14))
Вариант 2:
f={1:1}; g={1:1}
for n in range(2, 15):
f[n] = 2 * f[n - 1] + g[n - 1] - 2
g[n] = f[n - 1] + 2 * g[n - 1]
print(f[14] + g[14])
Определите, сколько символов * выведет эта процедура при вызове F(35):
def F( n ):
print('*')
if n >= 1:
print('*')
F(n-1)
F(n-2)
print('*')
96_631_265
Вариант 1:
def f(n):
global k; k += 1
if n >= 1: k += 1; f(n - 1); f(n - 2); k += 1
k = 0; f(35); print(k)
Вариант 2:
f = {-1:1, 0:1}
for n in range(1, 35 + 1): f[n] = 1 + 1 + f[n - 1] + f[n - 2] + 1
print(f[35])
Определите наибольшее трехзначное значение n, при котором значение F(n), будет больше числа 7. Запишите в ответе сначала найденное значение n, а затем через пробел – соответствующее значение F(n).
def F(n):
if n < 10: return n
else:
m=F(n // 10)
d=m % 10
if m < d: return d
else: return m
999 9
Вариант 1:
def f(n):
if n < 10: return n
else:
m = f(n // 10)
d = m % 10
if m < d: return d
else: return m
for n in range(999, 99, -1):
x = f(n)
if x > 7: print(n, x); break
Вариант 2:
f = {}
for n in range(10): f[n] = n
for n in range(10, 1000):
m = f[n // 10]
d = m % 10
f[n] = d if m < d else m
for n in range(999, -1, -1):
if f[n] > 7: print(n, f[n]); break
Определите наименьшее значение n такое, что последнее выведенное число при вызове F(n) будет больше числа 32. Запишите в ответе сначала найденное значение n, а затем через пробел – соответствующее значение F(n).
def F(n):
print(n)
if n>0:
d=n%10+F(n//10)
print(d)
return d
else: return 0
6999 33
Вариант 1:
def f(n):
global arr
arr.append(n)
if n: d = n % 10 + f(n // 10); arr.append(d); return d
else: return 0
for n in range(1, 10_000):
arr = []; x = f(n)
if arr[-1] > 32: print(n, x); break
Вариант 2:
f = {0:0}
for n in range(1, 10000):
x = n
if n > 0:
d = n % 10 + f[n // 10]
x = d
f[n] = d
else: f[n] = 0
if x > 32: print(n, f[n]); break
Определите наименьшее значение суммы n + m такое, что значение F(n, m) больше числа 15 и выполняется условие: n и m – разные натуральные числа. Запишите в ответе сначала значения n и m, при которых указанная сумма достигается, в порядке неубывания, а затем – соответствующее значение F(n, m). Числа в ответе разделяйте пробелом.
def F(n,m):
if n < m: n, m = m, n
if n != m: return F(n - m, m)
else: return n
16 32 16
def f(n, m):
if n < m: n, m = m, n
if n != m: return f(n-m, m)
else: return n
s = float('inf')
for n in range(1, 100):
for m in range(n + 1, 100):
x = f(n, m)
if x > 15 and n + m < s: print(n, m, x); s = n + m
Алгоритм вычисления функций F(n) и G(n) задан следующими соотношениями:
F(n) = G(n) = 1 при n = 1, F(n) = F(n – 1) + 3 ⋅ G(n – 1), при n > 1, G(n) = F(n – 1) – 2 ⋅ G(n – 1), при n > 1
Чему равна сумма цифр значения функции F(18) ?
46
Вариант 1:
def f(n): if n == 1: return 1 return f(n - 1) + 3 * g(n - 1) def g(n): if n == 1: return 1 return f(n - 1) - 2 * g(n - 1) print(sum(map(int, str(f(18)))))
Вариант 2:
f = {1:1}; g = {1:1}
for n in range(2, 18 + 1):
f[n] = f[n - 1] + 3 * g[n - 1]
g[n] = f[n - 1] - 2 * g[n - 1]
print(sum(map(int, str(f[18]))))
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n при n ≤ 3; F(n) = 2 ⋅ n ⋅ n + F(n – 1) при чётных n > 3; F(n) = n ⋅ n ⋅ n + n + F(n – 1) при нечётных n > 3;
Определите количество натуральных значений n, при которых F(n) меньше, чем 107.
92
Вариант 1:
def f(n):
if n <= 3: return n
if n % 2 == 0: return 2 * n ** 2 + f(n - 1)
return n ** 3 + n + f(n - 1)
k = 0
for n in range(1, 1000):
if f(n) < 10 ** 7: k += 1
print(k)
Вариант 2:
k, f = 0, {0:0}
for n in range(1, 100000):
if n <= 3: f[n] = n
else: f[n] = 2 * n * n + f[n - 1] if n % 2 == 0 else n ** 3 + n + f[n - 1]
if f[n] < 10 ** 7: k += 1
print(k)
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n ⋅ n + 3 ⋅ n + 9, при n ≤ 15 F(n) = F(n – 1) + n – 2, при n > 15, кратных 3 F(n) = F(n – 2) + n + 2, при n > 15, не кратных 3
Определите количество натуральных значений n из отрезка [1;1000], для которых все цифры значения F(n) чётные.
33
Вариант 1:
def f(n):
if n <= 15: return n * n + 3 * n + 9
if n % 3 == 0: return f(n - 1) + n -2
return f(n - 2) + n + 2
k = 0
for n in range(1, 1000 + 1):
if all(i not in str(f(n)) for i in '13579'): k += 1
print(k)
Вариант 2:
f = {-1: 7, 0: 9}
k = 0
for n in range(1, 1000 + 1):
if n <= 15: f[n] = n * n + 3 * n + 9
else: f[n] = f[n - 1] + n - 2 if n % 3 == 0 else f[n - 2] + n + 2
if all(c not in str(f[n]) for c in '13579'): k += 1
print(k)
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n + 15, при n ≤ 5 F(n) = F(n // 2) + n ⋅ n ⋅ n – 1, при чётных n > 5 F(n) = F(n – 1) + 2 ⋅ n ⋅ n + 1, при нечётных n > 5
Здесь «//» обозначает деление нацело. Определите количество натуральных значений n из отрезка [1;1000], для которых значения F(n) содержит не менее двух цифр 8.
164
Вариант 1:
def f(n):
if n <= 5: return n + 15
if n % 2 == 0: return f(n // 2) + n ** 3 - 1
return f(n - 1) + 2 * n ** 2 + 1
k = 0
for n in range(1, 1000+1):
if str(f(n)).count('8') > 1: k += 1
print(k)
Вариант 2:
k, f = 0, {}
for n in range(1, 1000 + 1):
if n <= 5: f[n] = n + 15
else: f[n] = f[n // 2] + n ** 3 - 1 if n % 2 == 0 else f[n - 1] + 2 * n ** 2 + 1
if str(f[n]).count('8') >= 2: k += 1
print(k)
Алгоритм вычисления функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = 1, если n < 3 F(n) = F(n – 1) + n – 1, если n > 2 и число n чётное, F(n) = F(n – 2) + 2 ⋅ n – 2, если n > 2 и число n нечётное
Вычислите значение F(34).
578
Вариант 1 (рекурсивная функция):
def f(n):
if n < 3: return 1
if n % 2 == 0: return f(n-1) + n - 1
return f(n - 2) + 2 * n - 2
print(f(34))
Вариант 2 (словарь):
f = {}
for n in range(1, 34 + 1):
if n < 3: f[n] = 1
else: f[n] = f[n - 1] + n - 1 if n % 2 == 0 else f[n - 2] + 2 * n - 2
print(f[34])
Алгоритм вычисления функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = 2, если n < 3 F(n) = 2 ⋅ F(n – 2) – F(n – 1) + 2, если n > 2 и число n чётное, F(n) = 2 ⋅ F(n – 1) – F(n – 2) – 2, если n > 2 и число n нечётное
Вычислите значение F(17).
358
Вариант 1 (рекурсивная функция):
def f(n):
if n < 3: return 2
if n % 2 == 0: return 2 * f(n-2) - f(n-1) + 2
return 2 * f(n-1) - f(n-2) - 2
print(f(17))
Вариант 2 (словарь):
f = {}
for n in range(1, 17 + 1):
if n < 3: f[n] = 2
else: f[n] = 2*f[n-2]-f[n-1]+2 if n%2==0 else 2*f[n-1]-f[n-2]-2
print(f[17])
Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n = 1 F(n) = n ⋅ F(n – 1), если n > 1
Чему равно значение выражения F(2023) / F(2020) ?
8_266_912_626
Ручное решение:
F(2023) = 2023 ⋅ F(2022) F(2022) = 2022 ⋅ F(2021) F(2021) = 2021 ⋅ F(2020) Объединяем три уравнения в одно: F(2023) = 2023 ⋅ 2022 ⋅ 2021 ⋅ F(2020) / F(2020) Отсюда: F(2023) = 2023 ⋅ 2022 ⋅ 2021 = 8266912626
Программное решение (словарь):
f = {1: 1}
for n in range(2, 2023 + 1): f[n] = n * f[n - 1]
print(f[2023] / f[2020])
Программное решение (рекурсивная функция):
from sys import *
setrecursionlimit(10_000)
def f(n):
if n == 1: return 1
return n * f(n - 1)
print(f(2023)/f(2020))
(К. Багдасарян) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n < 4 или число n нечётное, F(n) = F(n – 1) + F(n – 2) + F(n – 3), если n > 3 и число n чётное
Чему равно значение выражения F(2008) – F(2006)?
2
Ручное решение:
F(2008) = F(2007) + F(2006) + F(2005) Т.к. F(2007) = F(2005) = 1, получаем: F(2008) − F(2006) = 2 + F(2006) − F(2006) = 2
Программное решение (словарь):
f = {1: 1, 2: 1, 3: 1}
for n in range(4, 2008 + 1):
if n < 4 or n % 2 != 0: f[n] = 1
if n > 3 and n % 2 == 0: f[n] = f[n - 1] + f[n - 2] + f[n - 3]
print(f[2008] - f[2006])
Программное решение (рекурсивная функция):
def f(n):
if n < 4 or n % 2 != 0: return 1
return f(n-1)+f(n-2)+f(n-3)
print(f(2008)-f(2006))
(А. Куканова) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = √n, если √n – натуральное число, F(n) = F(n + 1) + 1, если √n – дробное число
Чему равно значение выражения F(4850) + F(5000)?
232
Вариант 1 (словарь):
f = {5041:71}
for n in range(5040, 4849, -1):
f[n] = int(n ** 0.5) if int(n ** 0.5) ** 2 == n else f[n + 1] + 1
print(f[4850] + f[5000])
Вариант 2 (рекурсивная функция):
def nn(x): return round(x**.5)**2 == x
def f(n):
if nn(n): return round(n**.5)
return f(n+1) + 1
print(f(4850)+f(5000))
(А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n = 1 F(n) = (2 · n - 1) · F(n – 1), если n > 1
Чему равно значение выражения F(3516) / F(3513)?
347_280_657_273
Вариант 1 (словарь):
f = {1:1}
for n in range(2, 3517): f[n] = (2 * n - 1) * f[n - 1]
print(f[3516] / f[3513])
Вариант 2 (рекурсивная функция):
from functools import *
@lru_cache(None)
def f(n):
if n == 1: return 1
return (2 * n - 1) * f(n - 1)
for n in range(1, 3517): f(n)
print(int(f(3516) / f(3513)))
Вариант 3 (рекурсивная функция):
from sys import *
setrecursionlimit(10_000)
def f(n):
if n == 1: return 1
return (2 * n - 1) * f(n - 1)
print(int(f(3516) / f(3513)))
(А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n = 1 F(n) = (3 · n + 5) · F(n – 1), если n > 1
Чему равно значение выражения F(2073) / F(2070)
240_757_875_872
Вариант 1 (словарь):
f = {1:1}
for n in range(2, 2074): f[n] = (3 * n + 5) * f[n - 1]
print(f'{f[2073] // f[2070]:,}'.replace(',', ' '))
Вариант 2 (рекурсивная функция):
from functools import *
@lru_cache(None)
def f(n):
if n == 1: return 1
return (3 * n + 5) * f(n - 1)
for n in range(1, 2074): f(n)
print(int(f(2073) / f(2070)))
Вариант 3 (рекурсивная функция):
from sys import *
setrecursionlimit(10_000)
def f(n):
if n == 1: return 1
return (3 * n + 5) * f(n - 1)
print(int(f(2073) / f(2070)))
(А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n = 1 F(n) = n·F(n – 1) + 1, если n > 1
Чему равно значение выражения F(3303) / F(3300)? В ответе укажите только целую часть числа.
36002376306
Вариант 1 (словарь):
f = {1:1} for n in range(2, 3304): f[n] = n * f[n - 1] + 1 print(f[3303] // f[3300])
Вариант 2 (рекурсивная функция):
from sys import *
setrecursionlimit(10_000)
def f(n):
if n == 1: return 1
return n * f(n-1) + 1
print(f(3303) / f(3300))
(К. Багдасарян) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n < 3 F(n) = F(n – 1) + F(n – 2), если n > 2
Чему равно значение выражения (F(1006) – F(1004)) / F(1005)?
1
Вариант 1 (словарь):
f = {n:n for n in range(3)}
for n in range(3, 1007): f[n] = f[n - 1] + f[n - 2]
print((f[1006] - f[1004]) // f[1005])
Вариант 2 (рекурсивная функция):
from functools import *
@lru_cache(None)
def f(n):
if n < 3: return 1
return f(n-1)+f(n-2)
for n in range(1, 1007): f(n)
print((f(1006) - f(1004)) // f(1005))
(К. Багдасарян) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, если n < 4, F(n) = n, если n > 3 и число n нечётное, F(n) = F(n – 1) + F(n – 2) + F(n – 3), если n > 3 и число n чётное
Чему равно значение выражения F(2254) – F(2252)?
4504
Вариант 1 (словарь):
f = {}
for n in range(2255):
if n < 4: f[n] = 1
elif n > 3 and n % 2 != 0: f[n] = n
else: f[n] = f[n - 1] + f[n - 2] + f[n - 3]
print(f[2254] - f[2252])
Вариант 2 (рекурсивная функция):
from functools import *
@lru_cache(None)
def f(n):
if n < 4: return 1
if n % 2 != 0: return n
return f(n - 1) + f(n - 2) + f(n - 3)
for n in range(1, 2255): f(n)
print(f(2254) - f(2252))
(К. Багдасарян) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 2, если n = 1, F(n) = 2 · F(n – 1), если n > 1
Чему равно значение выражения F(1900) / 21890?
1024
Вариант 1 (словарь):
f = {1:2}
for n in range(2, 1901): f[n] = 2 * f[n - 1]
print(f[1900] // 2 ** 1890)
Вариант 2 (рекурсивная функция):
from functools import *
@lru_cache(None)
def f(n):
if n == 1: return 2
return 2 * f(n - 1)
for n in range(1, 1901): f(n)
print(f(1900) // 2 ** 1890)
(А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n - 10000, если n > 10000, F(n) = F(n + 1) + F(n + 2), если 1 ≤ n ≤ 10000
Чему равно значение выражения F(12345) · (F(10) − F(12)) / F(11) + F(10101)?
2446
Вариант 1 (словарь):
f = {}
for n in range(12345, 0, -1):
if n <= 10_000: f[n] = f[n + 1] + f[n + 2]
else: f[n] = n - 10_000
print(f[12345] * (f[10] - f[12]) // f[11] + f[10101])
Вариант 2 (рекурсивная функция):
from functools import *
@lru_cache(None)
def f(n):
if n > 10000: return n - 10_000
return f(n + 1) + f(n + 2)
for n in range(12346, 0, -1): f(n)
print(f(12345) * (f(10) - f(12)) // f(11) + f(10101))
(А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n!, если n ≥ 5000, F(n) = 2 · F(n + 1) / (n + 1), если 1 ≤ n < 5000
Чему равно значение выражения 1000 · F(7) / F(4)?
Примечание. Факториал числа n, который обозначается как n!, вычисляется по формуле
n! = 1 · 2 · … · n
26250
Вариант 1 (словарь):
from math import *
f = {}
for n in range(5001, 0, -1):
if n >= 5000: f[n] = factorial(n)
else: f[n] = 2 * f[n + 1] // (n + 1)
print(1000 * f[7] // f[4])
Вариант 2 (рекурсивная функция):
from math import *
from functools import *
@lru_cache(None)
def f(n):
if n >= 5000: return factorial(n)
return 2 * f(n + 1) // (n + 1)
for n in range(5100, 0, -1): f(n)
print(1000 * f(7) // f(4))
(А. Кабанов) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n ≥ 10 000, F(n) = n / 4 + F(n / 4 + 2), если n < 10 000 и n делится на 4, F(n) = 1 + F(n + 2) , если n < 10 000 и n не делится на 4
Чему равно значение выражения F(174) – F(3)?
67
Вариант 1:
from sys import *
setrecursionlimit(10000)
def f(n):
if n>=10000: return n
if n % 4 == 0: return n // 4 + f(n//4 + 2)
return 1 + f(n + 2)
print(f(174) - f(3))
Вариант 2:
from functools import *
@lru_cache(None)
def f(n):
if n >= 10000: return n
if n < 10000 and n % 4 == 0: return n // 4 + f(n // 4 + 2)
if n < 10000 and n % 4 != 0: return 1 + f(n + 2)
for n in range(10000, 1, -1):
if n % 4 != 0 and n % 2 != 0: f(n)
for n in range(10000, 1, -1): f(n)
print(f(174) - f(3))
(Д. Статный) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n ≥ 10 000, F(n) = F(n + 1) + n2 – 3 · (n – 1) , если n < 10 000 и n чётное, F(n) = F(n + 2) + 4 · n + 1, если n < 10 000 и n нечётное
Чему равно значение выражения F(9950) – F(9999)?
99930181
Вариант 1:
def f(n):
if n >= 10000: return n
if n < 10000 and n % 2 == 0: return f(n + 1) + n ** 2 - 3 * (n - 1)
return f(n + 2) + 4 * n + 1
print(f(9950) - f(9999))
Вариант 2:
f = {10000:10000, 10001:10001}
for n in range(9999, 0, -1):
if n % 2 == 0: f[n] = f[n + 1] + n ** 2 - 3 * (n - 1)
else: f[n] = f[n + 2] + 4 * n + 1
print(f[9950] - f[9999])
(М. Байрамгулов) Алгоритм вычисления функции F(n, m), где n и m – натуральные числа, задан следующими соотношениями:
F(n, m) = 0, если m > n, F(n, m) = 1 + F(n, m + 1), если m ≤ n и n делится на m, F(n, m) = F(n, m + 1), если m ≤ n и n не делится на m
Чему равно значение выражения F(107864, 3)?
14
Вариант 1:
from sys import *
setrecursionlimit(1_000_000)
def f(n, m):
if m > n: return 0
if m <= n and n % m == 0: return 1 + f(n, m + 1)
if m <= n and n % m != 0: return f(n, m + 1)
print(f(107864, 3))
Вариант 2:
f = {(107864, 107865): 0}
for n in range(107864, 0, -1):
for m in range(107864, 0, -1):
if m > n: f[(n, m)] = 0; break
if m <= n and n % m == 0: f[(n, m)] = 1 + f[(n, m + 1)]
if m <= n and n % m != 0: f[(n, m)] = f[(n, m + 1)]
print(f[(107864, 3)])
Вариант 3:
Значение функции увеличивается на единицу, когда m является делителем числа n. Результатом программы будет количество делителей числа 107864, в диапазоне от 3 и до 107864, включительно.
x = 107864; a = set()
for i in range(3, x + 1):
if x % i == 0: a.add(i)
print(len(a))
(А. Бриккер) Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(n) = n – 1, при n ≤ 3; F(n) = F(n – 2) + n / 2 – F(n – 4), если n > 3 и n чётно; F(n) = F(n – 1) · n + F(n – 2), если n > 3 и n нечётно
Чему равно значение выражения F(4952) + 2 ⋅ F(4958) + F(4964)?
9920
from functools import *
@lru_cache(None)
def f(n):
if n <= 3: return n - 1
if n > 3 and n % 2 == 0:
return f(n - 2) + n // 2 - f(n - 4)
return f(n - 1) * n + f(n - 2)
for n in range(4965): f(n)
print(f(4952) + 2 * f(4958) + f(4964))
(Е. Джобс) Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(n) = n, при n ≤ 10 F(n) = 1, при n ≥ 10000 F(n) = n % 10 + F(n+2), при 10 < n < 10000 и четном n, F(n) = F(n–2) – (n–1) % 10, при 10 < n < 10000 и нечетном n
Чему равно значение выражения F(4500) + F(5515)? В ответе запишите только целое число.
Примечание: операция a % b находит остаток от деления числа a на число b.
4
Вариант 1:
fch = {10000:1}
for n in range(9998, 4500 - 2, -2):
fch[n] = n % 10 + fch[n + 2]
fn = {9:9}
for n in range(11, 5515 + 1, 2):
fn[n] = fn[n - 2] - (n - 1) % 10
print(fch[4500] + fn[5515])
Вариант 2:
#найдем значение f(4500) sch = 0 for n in range(4500, 10000+1, 2): if n < 10000: sch += n % 10 else: sch += 1 #найдем значение f(5515) sn = 0 for n in range(5515, -1, -2): if n > 10: sn += (n - 1) % 10 else: sn -= n; break print(sch - sn)
(Е. Джобс) Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(1) = 2, F(n) = F(n-1) · 3n % 5 / 3n % 7
Чему равно значение выражения F(1025) / F(1030)? В ответе запишите только целое число.
Примечание: операция a % b находит остаток от деления числа a на число b.
729
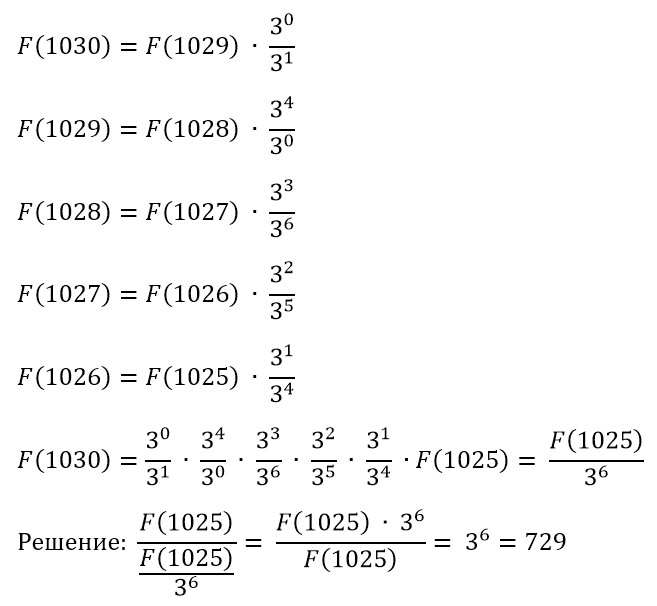
(А. Богданов) Обозначим частное от деления натурального числа a на натуральное число b как a // b, а остаток как a % b. Например, 17 // 3 = 5, 17 % 3 = 2. Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(n) = 0, если n < 10 F(n) = F(n // 10) + (n // 10 % 10) – (n % 10)
Найдите количество таких чисел, не превышающих 1010, для которых F(n) = 9.
111111111
Все числа, начинающиеся на 9 и окачивающиеся на 0 дают F(n) = 9 (можно убедиться, выполнив программу с числами в указанных диапазонах, например от 900 до 990, с шагом 10).
#учитываем 90 count = 1 #k - количество цифр 9 и 0 в минимальном и максимальном числе #например, первый диапазон: от 900 до 990 for k in range(2, 10): mx = int(k * '9' + '0') mn = int('9' + k * '0') count += (mx - mn) // 10 + 1 print(count)
Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(n) = 0, если n = 0 F(n) = F(n–1) + 2 · n
Найдите количество таких чисел в диапазоне от 100 000 000 до 200 000 000, для которых F(n) не делится на 3.
33333334
k = 0
for n in range(10 ** 8, 2 * 10 ** 8 + 1):
if n * (n+1) % 3 != 0: k += 1
print(k)
Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(n) = 0, если n = 0 F(n) = F(n – 1) + 5 · n
Найдите количество таких чисел в диапазоне от 189 456 678 до 567 654 321, для которых F(n) не делится на 7.
270141174
Числа, для которых F(n) делится на 7 - это n, с остатком 6 от деления на 7 или кратные 7. Находим все такие n в указанном диапазоне (первое с остатком 6 - 189456679, последнее кратное 7 - 56765319). Затем из общего количества чисел вычитаем найденное количество чисел.
k = 0 for n in range(189456679, 567654319, 7): k += 2 print(567654321 - 189456678 + 1 - k)
Обозначим частное от деления натурального числа a на натуральное число b как a // b, а остаток как a % b. Алгоритм вычисления функции F(n), где n – неотрицательное число, задан следующими соотношениями:
F(n) = 0, если n = 0 F(n) = F(n//10) + (n % 10)
Найдите количество таких чисел в диапазоне от 865 432 015, 1 585 342 628, для которых F(n) > F(n+1).
71991061
F(n) > F(n + 1) только для чисел, оканчивающихся на 9:
Пример: F(9) = 0 + 9 = 9 F(10) = 1 + 0 = 1 ... F(89) = 8 + 9 = 17 F(90) = 9 + 0 = 9 Ответ: (1585342619 - 865432019) / 10 + 1 = 71991061
Алгоритм вычисления функции F(a, b), где a и b – неотрицательные целые числа, задан следующими соотношениями:
F(a, b) = 0, если a = 0 и b = 0 F(a, b) = F(a–1, b) + b, если a > b F(a, b) = F(a, b–1) + a, если a ≤ b
Найдите количество таких чисел a, для которых можно найти число b, такое что F(a, b) = 2744000
112
Проанализируем рекурсивную функцию, выполнив вычисления для значения F(4, 4).
F(4, 4) = F(4, 3) + 4 = 12 + 4 = 16 F(4, 3) = F(3, 3) + 3 = 9 + 3 = 12 F(3, 3) = F(3, 2) + 3 = 6 + 3 = 9 F(3, 2) = F(2, 2) + 2 = 4 + 2 = 6 F(2, 2) = F(2, 1) + 2 = 2 + 2 = 4 F(2, 1) = F(1, 1) + 1 = 1 + 1 = 2 F(1, 1) = F(1, 0) + 1 = 0 + 1 = 1 F(1, 0) = F(0, 0) + 0 = 0 + 0 = 0 F(0, 0) = 0Можно заметить, что значение функции равно произведению её параметров, т.е. F(a, b) = a · b
a = set(); x = 2744000 sq = round(x ** .5) for i in range(1, sq + 1): if x % i == 0: a |= {i, x//i} print(len(a))
Таким образом, задача сводится к поиску количества делителей для числа 2744000.
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = n, при n ≤ 5, F(n) = n + F(n / 2 – 1), когда n > 5 и делится на 4, F(n) = n + F(n + 2) , когда n > 5 и не делится на 4
Назовите максимальное значение n, для которого возможно вычислить F(n).
12
def f(n):
if n<=5: return n
if n>5 and n%4==0: return n+f(n//2-1)
return n+f(n+2)
for n in range(100, 0, -1):
try:
print(n, f(n))
except:
...
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(1) = 1 F(n) = F(n/2) + 1, когда n ≥ 2 и чётное, F(n) = F(n - 1) + n, когда n ≥ 2 и нечётное
Назовите количество значений n на отрезке [1;100000], для которых F(n) равно 16.
5
def f(n):
if n == 1: return 1
if n % 2 == 0: return f(n // 2)+1
return f(n - 1)+n
k = 0
for n in range(1, 100_000 + 1):
if f(n) == 16: k += 1
print(k)
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(0) = 0 F(n) = F(n/2) + 3, при чётном n > 0 F(n) = 2·F(n - 1) + 1, при нечётном n > 0
Сколько различных значений может принимать функция F(n) при n, принадлежащих отрезку [1; 1000]?
348
def f(n):
if n==0: return 0
if n%2==0: return f(n // 2)+3
return 2 * f(n - 1) + 1
ans = set()
for n in range(1, 1000 + 1):
ans.add(f(n))
print(len(ans))
(А. Богданов) Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(0) = 0 F(n) = 1, когда 1 ≤ n < 3, F(n) = F(n - 1) + F(n - 2), когда n ≥ 3
Определите четыре последние цифры числа F(47)
5073
f={0:0, 1:1, 2:1}
for n in range(3, 48): f[n] = f[n - 1] + f[n - 2]
print(f[47])
(Е. Джобс) Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(n) = n + 3, при n ≤ 3 F(n) = F(n – 2) + n, при n > 3 и четном значении F(n-1), F(n) = F(n – 2) + 2•n, при n > 3 и нечетном значении F(n-1)
Определите сумму значений, являющихся результатом вызова функции для значений n в диапазоне [40; 50].
8508
f={n:n+3 for n in range(4)}
for n in range(4, 51):
if f[n - 1] % 2 == 0: f[n] = f[n - 2] + n
else: f[n] = f[n - 2] + 2 * n
s = 0
for n in range(40,51): s += f[n]
print(s)
(Е. Джобс) Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями:
F(0) = 1, F(1) = 3 F(n) = F(n–1) - F(n-2) + 3n, при n > 1
Чему равно значение функции F(40)? В ответе запишите только целое число.
126
f={0:1, 1:3}
for n in range(2, 41): f[n]=f[n-1]-f[n-2]+3*n
print(f[40])
(Е. Джобс) Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1, F(1) = 3 F(n) = F(n–1) – F(n–2) + 3n, при чётном n > 1 F(n) = F(n–2) – F(n–3) + 2n, при нечётном n > 1
Чему равно значение функции F(40)? В ответе запишите только целое число.
84
def f(n):
if n == 0: return 1
if n == 1: return 3
if n % 2 == 0: return f(n - 1) - f(n - 2) + 3 * n
return f(n - 2) - f(n - 3) + 2 * n
print(f(40))
(П. Волгин) Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1 F(n) = F(n – 1), при 0 < n ≤ 10 F(n) = 2,2 * F(n – 3), при 10 < n < 100 F(n) = 1,7 * F(n – 2), при n ≥ 100
Чему равно значение функции F(22)? В ответе запишите только целое число.
23
def f(n):
if n == 0: return 1
if 0 < n <= 10: return f(n - 1)
if 10 < n < 100: return 2.2 * f(n - 3)
return 1.7 * f(n - 2)
print(int(f(22)))
(А. Богданов) Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(n) = 0 при n ≤ 2 или n = 8 F(n) = 1 при n = 3 F(n) = F(n – 2) + F(n – 1) при n > 3 и n ≠ 8
Для какого значения n значение F(n) будет равно 25?
13
def f(n):
if n <= 2 or n == 8: return 0
if n == 3: return 1
if n > 3 and n != 8: return f(n - 2) + f(n - 1)
for n in range(1, 1000):
if f(n) == 25: print(n); break
Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(n) = 0 при n = 0 F(n) = F(n / 2) - 1 при чётных n > 0 F(n) = 1 + F(n – 1) при нечётных n > 0
Сколько существует чисел n, меньших 1000, для которых значение F(n) будет равно 0?
41
def f(n):
if n == 0: return 0
if n % 2 == 0: return f(n // 2) - 1
return 1 + f(n - 1)
k = 0
for n in range(1000):
if f(n) == 0: k += 1
print(k)
(П. Волгин) Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(n) = 1 при n ≤ 1 F(n) = 11·n + F(n - 1), если n > 1 и n чётное F(n) = 11·F(n - 2) + n в остальных случаях
Определите сумму четных значений F(n) для всех n на отрезке [35,50]. В качестве ответа запишите количество цифр в десятичной записи этой суммы.
Примечание: необходимо использовать арифметику многоразрядных чисел.
25
def f(n):
if n <= 1: return 1
if n % 2 == 0: return 11 * n + f(n - 1)
return 11 * f(n - 2) + n
s = 0
for n in range(35, 51):
sm = f(n)
if sm % 2 == 0: s += sm
print(s, len(str(s)))
Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1 F(n) = 1 + F(n - 1), если n > 0 и n нечётное F(n) = F(n / 2) в остальных случаях
Определите количество значений n на отрезке [1, 500 000 000], для которых F(n) = 3.
406
Нам подходят все числа у которых в двоичной СС только две единицы
from math import *
k = 0
for n in range(0, round(log(500_000_000, 2)) + 1):
for m in range(n + 1, round(log(500_000_000, 2)) + 1):
if 2**n + 2**m < 500_000_000:
k += 1
print(k)
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n ≥ 2025, F(n) = n + 3 + F(n + 3), если n < 2025.
Чему равно значение F(23) - F(21)?
1338
def f(n):
if n >= 2025: return n
return n + 3 + f(n + 3)
print(f(23) - f(21))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n ≥ 2025, F(n) = n + F(n + 2), если n < 2025.
Чему равно значение F(2022) - F(2023)?
2024
def f(n):
if n >= 2025: return n
return n + f(n + 2)
print(f(2022) - f(2023))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n < 11, F(n) = n + F(n-1), если n ≥ 11
Чему равно значение выражения F(2024) – F(2021)
6069
from sys import *
setrecursionlimit(10000)
def f(n):
if n < 11: return n
return n + f(n - 1)
print(f(2024) - f(2021))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 7, если n < 7, F(n) = n + 1 + F(n-2), если n ≥ 7
Чему равно значение выражения F(2024) – F(2020)
4048
from sys import *
setrecursionlimit(10000)
def f(n):
if n < 7: return 7
return n + 1 + f(n - 2)
print(f(2024) - f(2020))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 3, если n < 3, F(n) = 2n + 5 + F(n-2), если n ≥ 3
Чему равно значение выражения F(3027) – F(3023)?
12114
from sys import *
setrecursionlimit(10000)
def f(n):
if n < 3: return 3
return 2 * n + 5 + f(n - 2)
print(f(3027) - f(3023))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n > 2024, F(n) = n · F(n + 1), если n <= 2024
Чему равно значение выражения F(2022) / F(2024)?
4090506
def f(n): if n > 2024: return n return n * f(n + 1) print(f(2022) / f(2024))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 5, если n = 1, F(n) = 2n + 1 + F(n - 1), если n > 1
Чему равно значение выражения F(2024) - F(2022)?
8096
Вариант 1:
from sys import * setrecursionlimit(10000) def f(n): if n == 1: return 5 return 2 * n + 1 + f(n - 1) print(f(2024) - f(2022))
Вариант 2:
f = {}
for n in range(1, 2025):
f[n] = 5 if n == 1 else 2*n + 1 + f[n-1]
print(f[2024]-f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = 2·n·F(n - 1) при n > 1
Чему равно значение выражения (F(2024) – 4·F(2023)) / F(2022)?
16362024
f = {}
for n in range(1, 2025):
if n==1: f[n] = 1
if n>1: f[n] = 2 * n * f[n-1]
print((f[2024]-4*f[2023])//f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = n·F(n - 1) при n > 1
Чему равно значение выражения (2·F(2024) + F(2023)) / F(2022)?
8191127
f = {}
for n in range(1, 2025):
if n==1: f[n] = 1
if n>1: f[n] = n * f[n-1]
print((2*f[2024]+f[2023])//f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = 3·n·F(n - 1) при n > 1
Чему равно значение выражения (F(2024)/6 + F(2023)) / F(2022)?
6147897
f = {}
for n in range(1, 2025):
if n==1: f[n] = 1
if n>1: f[n] = 3 * n * f[n-1]
print((f[2024]//6+f[2023])//f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = 2·n·F(n - 1) при n > 1
Чему равно значение выражения (F(2024)/16 - F(2023)) / F(2022)?
1019592
f = {}
for n in range(1, 2025):
if n==1: f[n] = 1
if n>1: f[n] = 2 * n * f[n-1]
print((f[2024]//16-f[2023])//f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = (n + 1)·F(n - 1) при n > 1
Чему равно значение выражения (F(2024) - 3·F(2023)) / F(2022)?
4092528
f = {}
for n in range(1, 2025):
if n==1: f[n] = 1
if n>1: f[n] = (n + 1) * f[n-1]
print((f[2024]-3*f[2023])//f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = (n + 1)·F(n - 1) при n > 1
Чему равно значение выражения (F(2024) + 3·F(2023)) / F(2022)?
4104672
f = {}
for n in range(1, 2025):
if n==1: f[n] = 1
if n>1: f[n] = (n + 1) * f[n-1]
print((f[2024]+3*f[2023])//f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1, при n = 1; F(n) = (n - 1)·F(n - 1) при n > 1
Чему равно значение выражения (F(2024) + 2·F(2023)) / F(2022)?
4094550
f = {}
for n in range(1, 2025):
if n == 1: f[n] = 1
if n > 1: f[n] = (n - 1) * f[n - 1]
print((f[2024] + 2 * f[2023]) / f[2022])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = F(n/2) + 5, если n чётное; F(n) = F(n/3) + 4, если n нечётное и делится на 3; F(n) = 0, если n нечётное и не делится на 3.
Определите минимальное значение n, для которого F(n) = 108.
9437184
f={}
for n in range(1, 10_000_000):
if n%2==0: f[n] = f[n//2] + 5
else:
if n%3==0: f[n] = f[n//3] + 4
else: f[n] = 0
if f[n] == 108:
print(n)
break
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = F(n/2) + 5, если n чётное; F(n) = F(n/5) + 2, если n нечётное и делится на 5; F(n) = 0, если n нечётное и не делится на 5.
Сколько различных значений принимает функция F(n) на отрезке [1; 1000000]?
9437184
f={}; ans = set()
for n in range(1, 1_000_000+1):
if n%2==0: f[n] = f[n//2] + 5
else:
if n%5==0: f[n] = f[n//5] + 2
else: f[n] = 0
ans.add(f[n])
print(len(ans))
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n < 5; F(n) = 2n · F(n - 4), если n ≥ 5.
Чему равно значение выражения (F(13766) – 9·F(13762)) / F(13758)?
757543052
f={}
for n in range(1, 13800):
if n < 5: f[n] = n
if n >= 5: f[n] = 2*n * f[n-4]
print((f[13766] - 9*f[13762]) / f[13758])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n)=1 при n ≤ 5; F(n)=n+F(n–2), если n > 5.
Чему равно значение выражения F(2126) – F(2122)?
4250
f={}
for n in range(1, 2150):
if n <= 5: f[n] = 1
if n > 5: f[n] = n + f[n-2]
print(f[2126] - f[2122])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n при n < 20; F(n) = (n - 6) × F(n – 7), если n ≥ 20.
Чему равно значение выражения (F(47872) - 290 × F(47865)) / F(47858)?
2276939784
f = {}
for n in range(1, 47_900):
if n < 20: f[n] = n
if n >= 20: f[n] = (n - 6) * f[n-7]
print((f[47872] - 290 * f[47865]) / f[47858])
Алгоритм вычисления значения функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, при n ≤ 7 F(n) = G(n-3) * 3, если n > 7 G(n) = n, при n ≤ 7 G(n) = G(n-1) + 4, если n > 7
Чему равно значение выражения F(43000)
515901
f={}; g={}
for n in range(1, 43100):
if n <= 7:
f[n]=n; g[n]=n
if n > 7:
f[n]=g[n-3] * 3
g[n]=g[n-1] + 4
print(f[43000])
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n при n < 10; F(n) = 3n + F(n - 3), если n ≥ 10.
Чему равно значение выражения (F(6250) + 2×F(6244)) / F(6238)? В ответе запишите целую часть полученного числа
3
f = {}
for n in range(1, 6300):
if n < 10: f[n] = n
if n >= 10: f[n] = 3*n + f[n - 3]
print((f[6250] + 2 * f[6244]) // f[6238])
Алгоритм вычисления значения функции F(n) и G(n), где n – целое число, задан следующими соотношениями:
F(n) = 2×(G(n - 3) + 8); G(n) = 2×n, если n < 10. G(n) = G(n - 2) + 1, если n ≥ 10.
Чему равно значение выражения F(15548)
15588
f = {}; g = {}
for n in range(1, 16000):
if n > 3: f[n] = 2 * (g[n - 3] + 8)
if n < 10: g[n] = 2 * n
if n >= 10: g[n] = g[n - 2] + 1
print(f[15548])
Алгоритм вычисления значения функции F(n) и G(n), где n – целое число, задан следующими соотношениями:
F(n) = G(n - 1) + G(n - 3); G(n) = 3×n, если n ≤ 9. G(n) = G(n - 4), если n > 9.
Чему равно значение выражения F(42999)
43032
f = {}; g = {}
for n in range(1, 43100):
if n > 3: f[n] = g[n - 1] + g[n - 3]
if n <= 9: g[n] = 3 * n
if n > 9: g[n] = g[n - 4] + 2
print(f[42999])
Алгоритм вычисления значения функции F(n) и G(n), где n – целое число, задан следующими соотношениями:
F(n) = G(n - 3); G(n) = n, если n ≤ 20. G(n) = G(n - 2) + 1, если n > 20.
Чему равно значение выражения F(25000)
12508
f = {}; g = {}
for n in range(1, 25100):
if n > 3: f[n] = g[n - 3]
if n <= 20: g[n] = n
if n > 20: g[n] = g[n - 2] + 1
print(f[25000])
Алгоритм вычисления значения функции F(n) и G(n), где n – целое число, задан следующими соотношениями:
F(n) = G(n - 1); G(n) = 3 * n, если n ≤ 9. G(n) = G(n - 2) + 1, если n > 9.
Чему равно значение выражения F(47995)
24017
f = {}; g = {}
for n in range(1, 48000):
if n > 1: f[n] = g[n - 1]
if n <= 9: g[n] = 3 * n
if n > 9: g[n] = g[n - 2] + 1
print(f[47995])